Predicting US Production with Gaussians
Posted by Stuart Staniford on January 8, 2006 - 4:49am

EIA Field production of crude in the US, logistic (Hubbert) fit based only on 1930-1976 data, and Gaussian fit based on same time interval. Source: EIA for the data.
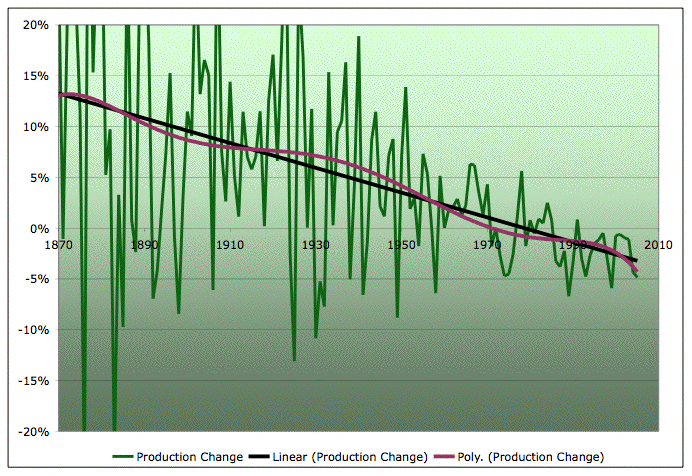
Year-on-year change in EIA Field production of crude in the US, with linear and sixth order polynomial fit. Source: EIA for the data.
That's not what the logistic would say - the logistic would call for an S shaped decline in the growth rate, starting at K (which is around 6%). Of course, we know the logistic is not that great at modeling the early production. Still, that straight line is really sticking out. Hmmm. Scratch head, write a few equations, turns out that the function that has a linearly decreasing growth rate is a Gaussian. I've vaguely heard of people using Gaussian's instead of logistics as models of the peak, but haven't played with it myself before tonight.
So, plot the log of production versus time and fit a parabola: Oh my.
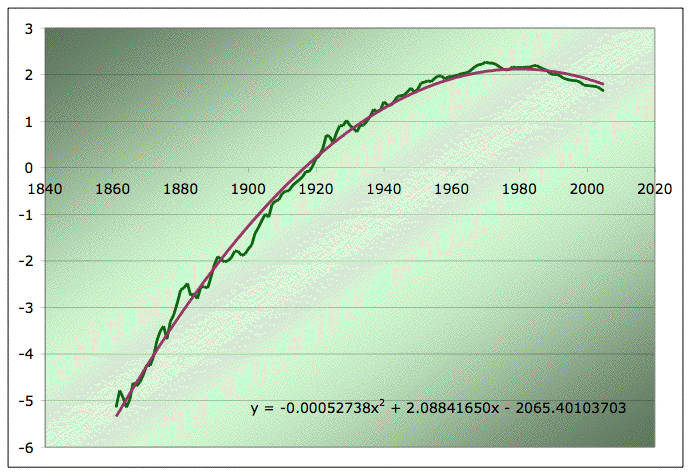
Natural log of EIA Field production of crude in the US, with quadratic fit. Source: EIA for the data.
Pretty good fit across the whole range. There's a very famous theorem in statistics (the central limit theorem) which says roughly that if you add a whole bunch of variables together which are identically distributed, the resulting sum will have a Gaussian distribution. You could argue that something similar is causing this, but the the things being added together are not obviously identically distributed. It's not clear to me why the central limit theorem would apply to a dynamical process in time - the time profile of oil production is not a statistical sampling process, it's an economic/stochastic/sociological spread process through a complex geologic reality. More thought required here.
There must be references on this surely. But I haven't found them in my literature search to date, and can't quickly find them now. Anyone?
Anyway, to get a quick feel for prediction, I repeated the thing I did Thursday night of seeing what would happen if you were to use the model to predict production forward:

EIA Field production of crude in the US, logistic (Hubbert) fit based only on 1930-1976 data, and Gaussian fit based on same time interval. Source: EIA for the data.
Yikes. That's really good. Not sure if the Gaussian will always do so well, but this is certainly interesting...



A simple Hubbert curve may be ideally applied only in the following cases:
3) Where a single geological domain having a natural distribution of fields is considered, political boundaries should be avoided.
OK, now in Laherrere's paper, he has examples from the FSU (former Soviet Union). And then, there is this later paper from Petroleum Review Is FSU oil growth sustainable? (pdf). He includes this linearization
But the FSU comprises several different oil provinces--West Siberia, Caspian Sea Basin, East Siberia, Arctic discussed by Colin Campbell in The Status of Oil and Gas Depletion in Russia (Dec 2004). Here's a map I found just give people a visualization.
Click to enlarge
Below, westexas argues that Alaska should not be thrown in with the Lower 48--"Alaska might as well be in the Middle East". We wouldn't take Mexico, lump that together with Angola, and do a Hubbert style analysis, logistic or Gaussian, of both together.
When modeling just the lower-48 (like Laherrere does) Hubbert's curve fits better than the Gaussian. These curves are somewhat different from one another, especially for the late inflexion first inflexion in Hubbert's.
Although quite not sure (haven't got there yet), Central Limit Theorem applies also to the logistic case.
As for your doubts on why these models fit so well, I'd like to look again to the population issue. Remember the logistic spreading of the sasser virus? I guess you know that's the way living things grow over time. Now, you should know that since the early eighties that world oil production per capita is flat.
An Analysis of US and World Oil Production Patterns Using Hubbert-Style Curves, Albert A. Bartlett, Mathematical Geology, V32, N1, Jan. 2000.
He used three variables: the estimated ultimate recovery (EUR), the date of the peak (tM), and the width of the gaussian (S). He then minimized the root mean square deviations between the data and the fit to find the EUR. He also looked at the sensitivity of his model to changes in tM and S and the uncertainty of the EUR, as well as per capita oil production, and R/P ratios. At the end of the paper, he compares his results with those of other researchers.
So, what's your take on the linearization prediction of 2.3 trillion barrels for world URR now that you've done this analysis?
http://www.hubbertpeak.com/bartlett/hubbert.htm
http://dieoff.org/page187.htm
and here's an interesting discussion of linearlization and Gaussians in a presentation:
http://www-physics.mps.ohio-state.edu/~aubrecht/AAPTSU02oil.pdf
Also, an important condition is that the variables must be independent (in short i.i.d.).
There are many variants of the Central Limit Theorem. One interesting formulation is the following (from the link you gave on wikipedia):
It's not easy to formulate the oil production problem in a strictly probabilistic framework. Curve fitting used here is a parameteric regression approach. An alternative approach is the nonparametric density estimation (or regression). It consists in estimating an unknown density function from a sum of kernel functions:
where h is the smoothing parameter and K(x) is the symmetric kernel function which must satisfy the following properties:
This formulation is attractive because K(x) can be interpreted as an elementary field production curve. Furthermore, you don't need to make assumpations about the shape of the curve (gaussian, logistic, etc.). For more info, here a quick introduction. I tried once a few simulations by adding elementary curves spawn by a prior model which was supposed to model the discovery pattern:
A Statistical Model for the Simulation of Oil Production
The two best case histories are the Lower 48 and the North Sea. Together, these two regions account for close to 20% of all oil produced to date worldwide. The Lower 48 peaked at 48% of Qt, and the North Sea peaked at 52% of Qt--an average of 50%. The world reached 50% in 2005, and the two facts we know are: (1) oil traded at record high nominal price levels in 2005 and (2) oil production year over year is flat. Both facts are consistent with a peak.
I have a suggestion for an experiment. You can easily plot the North Sea data, using the EIA data at the following website: http://www.eia.doe.gov/emeu/ipsr/t41b.xls
Note that this is crude + condensate production. In my opinion, using NGL's distorts the data because NGL's can easily come from gas reservoirs in addition to oil reservoirs (as can condensates, but that is a lesser factor).
North Sea production starts in 1971. We know that they peaked in 1999 at just a hair under 6 mbpd. You plot annual production (P) divided by cumulative to date (Q) versus Q. I think that I used a P/Q limit of about 20% (0.20) on my plot. I suggest that everyone generate their own plot, do a best linear fit and come up with your own Qt. I came up with 60 Gb. Stuart could then compare the answers.
Parsimony of model is nice, but so is good fit...we're looking for models that are generalizable to all the units of analysis...more importantly if we can discern many models that fit relatively well but vary across the cases, then we can use model selection, and the assumptions behind each model, to start figuring out WHY the countries vary...
I continue to think that including Alaska with the Lower 48 is a mistake. In terms of both geology and timing of development (the Lower 48 peaked before serious production even began in Alaska), Alaska might as well be in the Middle East. Alternatively, you could plot all of North America.
http://www.eia.doe.gov/emeu/security/topexp.html
There are 12 countries on this list. The total net exports of those countries exporting less than one mpbd is not significant. Note that the big three--Saudi Arabia; Russia and Norway--acount for more than 50% of the exports from the top 12 countries.
Two of the countries--Saudi Arabia and Norway--are past their 50% of Qt marks--and both countries show declining production from 2003. Russia's production is flat year over year (I have never seen P/Q versus Q plot for Russia).
Total world oil production is interesting, but exports make the world go around. With the top three either declining or showing flat production, where will the oil production come from to meet current, let alone future, export demand? I think that this topic has been underexplored.
Note that Saudi Arabia's net 2003 exports were alone basically equal to the sum of the bottom six on the top 12 list.
If we could get a Russian P/Q versus Q plot, we could take a stab at predicting the net exports from the big three over the next 5-10 years. It ain't going to be pretty. I suppose that it would make sense to lump the Soviet Union, Russian and FSU data in to one data file.
I agree. Rick and I have had some discussions about writing something up on the importance of exports and the fungibility of oil. I had taken an initial stab at it when I wrote Algeria, Land of Opportunity? I see that Algeria is #11 on EIA's 2003 list. They are a mid-level producer that would not seem very important in the overall scheme of things but they are in terms of exports. You'll notice that Canada, for example, is not on the list.
dave..i have been thinking about fungibility of oil also, as have many other posters..i like to look at various events and put them together in a "big picture" view. i'd like feedback on other TOD's views of this.
i am fascinated by what has happened in the last week in this regard. i think there are two interacting cross currents going on now in world politics.
...first, the fading idea that the u.s. is a superpower, to be feared at all costs. the iraq war and it's consequences are eliminating that fear. like the vietnam war, the aftereffect will be a distaste in american minds for foreign involvement.
so what, you say....the second crosscurrent..if countries that control oil and finance consider themselves outside of the u.s. influence, they will begin to act in their own self interest, including how they foresee parsing out their remaining,dwindling oil supplies . four cases in point from the last week:
one...russia's treatment of the ukraine, and it's potential shot across the bow of europe (and possibly the u.s.)
two...the reversal of OPEC in their decision to reduce supply:
..no more we'd like to see oil at $40-50 a barrel
three...rumblings in brazil that oil supply should be limited as posted by alan yesterday
and finally... the economic blockbuster, first posted by geopoet, about china moving it's investments out of the dollar
...individually, they are, IMHO, surprising events, but taken together , in such a short time scale...i think they represent a substantial shift in worldview.
comments?
Ukraine wants to be 'western' and turn its back on Russia, then let them pay western market prices.
OPEC would mostly rather make as much money by pumping less rather than (in Saudi's case) be exposed as not having swing production capacity.
Brasil is a growing and developing nation, it does not wish to sell itself into greater future poverty for short term profiteering. Treason seems a most appropriate term.
China has more $ denominated assets than it is comfortable with (given it will pull the rug from under the $ someday), diversification mandatory - and has been happening softly for near a year.
They are but the initial ripples of 'end of empire'. The US one has been brief, a mere 100 years, but those who watch such things know it is coming within 20 years. Perhaps you are seeing these events as 'at odds' with the current system - as determined by the USA - and should rather see them as rational symptoms of the ending of that system and US hegemony.
Past such events have always been bloody and the odds strongly favour that this time too. We will have to grow up very fast to avoid it, the signs bode ill.
I might have been one of those suggesting that a guassian fit would be better (based in part on what Deffeyes has said), but this all gets me to thinking.
What are we really learning by doing this? There will always be some noise in the data for various reasons that this type of curve fitting will never tell us. There could be an economic downturn that could suppress demand. The hurricanes last year would have caused a bit of a blip. A terrorist attack (for that matter the insurgents in Iraq are effectively cutting off Iraq's oil supply).
So at the end of the day, do we get a more accurate guess as to when the peak will be, or the depletion rates we will see in the future?
Still, your point about exogenous events is a good one. Exogenous events are (cough trite alert) tough to predict, but at least we have a good idea of what exogenous events are possible and their probability of actually occurring, save the actual reserve numbers.
Makes me start thinking Bayes...you know?
This is news to me. If we did...
Re: "Makes me start thinking Bayes...you know?"
then I'd be thinking Bayes too. Wanna expand on this a bit, PG?
in better words, with Bayes, you assign prior probabilities to events you wish to control for...they are still guesses, but they can at least be informed guesses...
I am still learning it, to be honest. I've played with it a bit in some of my professional work, but I am by no means an expert.
http://en.wikipedia.org/wiki/Bayes%27_theorem
Unfortunately it is the relatively low probability events, very hard to predict rationally in advance, that mostly shape the critical turning points of our 'machine'. How would the world have turned had an archduke not been shot in Sarajevo and a different event triggered WWI a year or so later or earlier? The map of Europe would likely have been somewhat different today, as might subsequent history.
The best we can probably do is know the critical times, when things are in delicate balance or imbalance and relatively small events might overturn nearly everything. Sometimes the balance can be restored, sometimes not and events take their own course, beyond reason, modelling and human control. Yes, we can guess, speculate, model, predict rationally or less rationally at such times but, if we are honest, we would admit that we are really doing so as a 'comfort', knowing that we are occupying time while reality crystallizes into its new form.
I know, you probably know, we have entered such a critical time. Something relatively unexpected could happen today, tomorrow, in a year or so's time, and reality as it has been for 40 or more years may be gone, the rules changed, the challenges new. We also know this is very likely to be a big one. And we know the chances are getting significant and growing.
Sharon's stroke has changed future probabilities somewhat, at first look it seems to the short term 'safer' side. But there are other potential events in the next few months which may trump that. Sometimes I wish I knew but other times my rational side dominates and I am just afraid (not irrationally so). Fortunately or not my 'irrational' side is usually more likely to be right, and so I continue to listen to it.
So, back to the subject. There is nothing wrong with using Bayesian techniques to evaluate probabilities of potential events, I would say do it with all fervour. But do remember that amongst the many events with less than 10% probability lurk a big handful which would change everything at the 'right' moment. Perhaps some way of modelling the sum of them by year might result in the most useful analysis.
if I become 95% sure that a 5% probability event of an 8 magnitude (play numbers, but bear with me) will occur in the next five years, and that has changed from a 75% certainty of 10% of a 9...and I have some theoretical expectation of the things that certain event will affect, have I not gained explanatory power on my dependent variable, even if it is a latent variable such as the probability of oil being at $100?
I 'waste' some of my time trying to 'see' the possible futures, trying to work out when critical points might be, guessing at what they are, their causes and consequences, sometimes attempting to influence now to affect then. Objectively I would call that mad, but evidence seems to suggest some validity; truly mad, LOL.
I think it may be difficult to use Bayesian methods to model (in advance) what is really critical. My understanding is that it is hard to apply to a large group of low probability events in an effective way, but I would be very interested if you can show otherwise - then we might try to produce a list of potential events and assign probabilities.
How can we use Bayesian methods to model n1 to n99+ events with probabilities p1 to p99+ (where pn is < 0.1) such that we can say p[all] is >= 0.95?
For now I would say that, as a rough approximation, the odds of a massively disruptive event in 2006 is about 30% which will increase by about 50% of the prior year, year on year. If by 1st Jan 2010 things are mostly as they are today I will be completely astonished (I have never been completely astonished in my 51 years of life).
Right. Or production. Westexas brought up a linearization for Russia. So, I looked around a bit. EIA production data starts in 1991--that's not too surprising. The BP data starts in 1985 and thinking of PG's exogenous events (there's a euphemism if I ever heard one!) -- here's Russian production.
Click to enlarge
The biggest mystery to me is this: why the symmetry? Why the heck is the down side a mirror of the up side? I don't see a reason in the world why that would be true, in everything I can think of suggests that it should not be.
During the growth phase, production is limited at first by the costs of new investment and by alternative opportunities for investment capital. As the field develops, production growth begins to slow down. The field is approaching "maturity" and the owners are not investing that much more into it. Maybe it is saturated in terms of reasonable places to put in new wells, or at least the cost of adding more equipment won't be paid back in the lifetime of the field.
Eventually production peaks, which seems to be largely a physical limitation. You just can't suck oil out faster at a reasonable cost. (It's worth noting that this may not be the reason, it may be that you could suck oil out faster, but the cost of adding more equipment to do this would not be paid back in the relatively short remaining lifetime of the field - in that case, the owners in effect decide to let the field peak in order to maximize their profits.)
And then we're on the decline, which now seems to be purely physical. We're not adding or removing wells, but the oil is getting harder and harder to suck out. Every year we get less.
So here is the mystery again: the decline seems to be primarily a physical process based on the reluctance of oil to be pulled out of the rock. But the growth phase seems to be largely economics-based. The rate of production growth is limited by economic decisions about how much to invest in the field at each point in its lifetime. I don't see why these two phases should mirror each other.
In terms of Stuart's graph above, this translates into why the slope of the fitted line is constant as it crosses the horizontal axis. Why does the decrease in production growth rate (a confusing concept, the third derivative of oil remaining!) remain the same post-peak as pre-peak?
One problem is that only a small portion of the line is below the axis. The U.S. is only slightly past its peak when we look at the whole history. It would be interesting to apply the analysis to a single field, one that peaked long ago, to see how well the right side of the production curve mirrored the left side.
Either way, the area under the curve is finite...but that's also why the reserve numbers are such a big deal. In the US we have a good idea of how much petroleum we have left, so this all works quite well...we're just trying to fit this, so that we can generalize to other countries where we have less complete information.
Models derived from the mechanics/physics of the phenomena of interest might be percieved as more legitimate, yet they are only as good as the number of factors they take into account. In physical models the nagging question is whether some mechanism was overlooked and not included in the model.
Another interesting problem is when a model can correctly predict outcomes, yet is still wrong. Take Maxwell's equations on light propagation. Here the equations were correct, yet the Maxwell's concept of light propagating through an either was wrong.
With regards to oil, if it can be shown that most oil fields follow a similar pattern (barring govenment collapse or war) then that should be convincing on its own. One need only assemble data on many oil fields.
But then, when we look at the whole U.S. we are adding up all the contribution from all the fields, and as a general principle, adding a bunch of independent, hump-shaped distributions will tend to produce a Gaussian? And this summation will be symmetric? Does that work?
There is no guarantee that this kind of summation will produce a gaussian or a symmetric curve. I believe that it has to do with the time of production start that is a random variable with an unknown distribution related to the discovery curve. We can however make the following observations:
- the distribution of field size follow roughly a lognormal distribution which implies that you have very few big fields and a lot of small fields.
- big fields were discovered first and exploited first.
- there is a lot of overlap between the lifetime of indiviual fields (discoveries are concentrated in time).
These conditions must play a role in the shape of the observed total production curve.AFAIK, no one has been able to confirm correlations in discoveries from year to year.
http://mobjectivist.blogspot.com/2006/01/would-you-believe.html
A partial explanation, considering a single well: as pressure declines so will oil exuded, that has a mathematical shape based on pressure, viscosity etc. This can be enhanced by various methods (pumping water into reservoir, reducing viscosity using steam, etc) but these cost energy and money so the well ultimately becomes unviable due to energy and / or money ROI. These things would apply to virtually all individual wells so is relatively straightforward to model.
When summed over a field these basics should result in a relatively fairly smooth and modelable shape. Once one goes beyond a single field it could be one is adding apples and pears. However, mathematical modelling is essentially an exercise in pragmatism: what predicts best works.
I would say the more 'interesting' area to question is the upslope. Why do fields seem to ramp up in a smooth way? I'd bet the answer is: they really don't, LOL, at least not consistently (just consider the fundamentals). I'd be inclined to bet that the downslope is more predictable and smooth than the upslope. So you are right to question the symmetry but I would bet the symmetrical approximation has more validity on the downslope than the upslope. I think we are probably past giving a f*ck about the upslope, perhaps that signifies something?
Interestingly enough, M. King Hubbert did the mathematical derivation of a number of equations for flow in porous media that are used in both groundwater and the oil patch.
Phx, AZ
Well drilling is not linear. A field starts with one rig, some time passes, then a second is added, at which point twice the number of wells are drilled/unit time. If the field warrants, a third etc is added. All rigs continue until all allocated hole locations have been drilled, including any involved with field expansion. In a large field, the first wells might be plugged, or use to dispose of salt water waste, etc.
At this point production has decayed but continues. Now, the (US) field might be sold to a small E&P because production is becoming more labor intensive. Then, some wells are maybe used for water injection (secondary production), other wells are re-worked.
I'm not much of a catastrophist, but I'm kind of afraid that the answer might be 'because humans with oil act a whole lot like yeast with sugar'.
Now if we can only manage the part where we end up with beer. ;)
Actually, the pseudo-gaussian behavior is easy to account for if you assume accelerated oil discoveries over time, i.e. d2D/dt2 = k. Remember, that the bulk of oil discoveries were made in the mid 1900's. And then you need to apply the oil shock model, which effectively modulates the extraction rate due to stochastic delays in the system.
This will also account for the values in 1859 and 1860, as the oil shock model formulation obeys causality.
The rate equation of the gaussian that you mentioned gives a degenerate solution of P(t) = 0. You have to give it a forcing function in 1859 to initiate causality. However once you do this, you won't have a gaussian solution, or at least it won't be something you can analytically produce. Same holds true of the logistic curve.
However, I think the period immediately preceding peak will be abnormal, too. Essentially we are making a transition from a mostly economic model to a mostly geologic resource limited model. I think this is visible in some of your previous analysis here, Stuart. Production that is mothballed and / or can be rapidly ramped up mostly has been, now the geologic and logistic determinants of increased production have become the determinants.
The peak and downslope are likely to be 'polluted' too. Countries will 'manage' production so it is not brought onstream and exported so as to protect their own future. A comment here today on Brasil and possible signs from Russia I would quote as the first symptoms of this.
Peak will probably be confusingly noisy for these reasons.
It wasn't meant to be easy, but us monkeys were meant to be smart, LOL.
Actually independence of the random variables is more essential than being identically distributed. Take for example the
Lindeberg-Feller theorem
Maybe the per-well cross-section is non-normal, but when you aggregate them, you get something more normal. (Ditto for the "sociological cross-section", etc. CLT is precisely about aggregation across independent events.) The time profile of oil production isn't exactly a sampling process, but the timing of oil strikes is more plausibly statistical in nature. It's a sort of sampling of the Earth's random distribution of oil deposits. And once oil is found, the way it is extracted is probably broadly similar with a few parameters to do with the size of the find etc. which themselves are randomly distributed.
I wonder if random walk type arguments work better here. If we consider the oil discovery and development process to be like a random walk (through a very complex abstract topology of oil plays and fields in which distance is some amalgam of physical distance and "conceptual" distance as a play) can we get somewhere. The model is basically to view the oil industry as a diffusion process through the oil bearing landscape. Random walks in Euclidean space have a gaussian density in distance from the origin, which spreads out over time - there's an exp(-x^2/t) type behavior. Could that give rise to an e(-t^2) behavior as it crosses the main oil bearing parts of the topology?
I don't know - seems like the industry is not random - we'd have to model the economics of fields as representing different probablities of going one way versus another in the oil bearing topology.
src: "Twilight in the desert" in the appendix B (p. 374 and 375)
Some 4,400 small fields produce more than 50% of the toal production. I think that reasonably we can assume than these small fields are relatively decorrelated in term of production profile and maturity (even if locally in time and space they are some correlations). The number of wells drilled must also be a factor, the US has 533,000 oil wells, averaging less than 17 barrels/well/day compared to 750 wells for Saudi Arabia -- averaging more than 12,000 barrels/well/day. There is a good chance that Saudi Araiba will never have a gaussian like production profile.
It isn't obvious how to apply such ideas to oil production over time, but that might be the most relevant mathematics to try to apply. The production curve might be expressible as a simple function of the set of vertices which are active (explored deposits) thereby transforming a statement about limiting shape of the subgraph into a statement about the production curve. Note that the limit here is in a rescaling parameter on the model, not time per se.
Even if the math is applicable, I suspect the result you'd find is roughly that for "large planets, with large oil deposits and large oil industries", the shape gets close to gaussian. There would also have to be a ton of assumptions about how to model the geology and economics. Still, I don't know that the heuristic argument for using a logistic curve is any better.
It isn't obvious how to apply such ideas to oil production over time, but that might be the most relevant mathematics to try to apply. The production curve might be expressible as a simple function of the set of vertices which are active (explored deposits) thereby transforming a statement about limiting shape of the subgraph into a statement about the production curve. Note that the limit here is in a rescaling parameter on the model, not time per se.
Even if the math is applicable, I suspect the result you'd find is roughly that for "large planets, with large oil deposits and large oil industries", the shape gets close to gaussian. There would also have to be a ton of assumptions about how to model the geology and economics. Still, I don't know that the heuristic argument for using a logistic curve is any better.